India RMO 1991 Q1

1. Problem

Let P be an interior point of a triangle ABC and AP, BP, CP meet the sides BC, CA, AB in D, E, F respectively. Show that

2. Solution

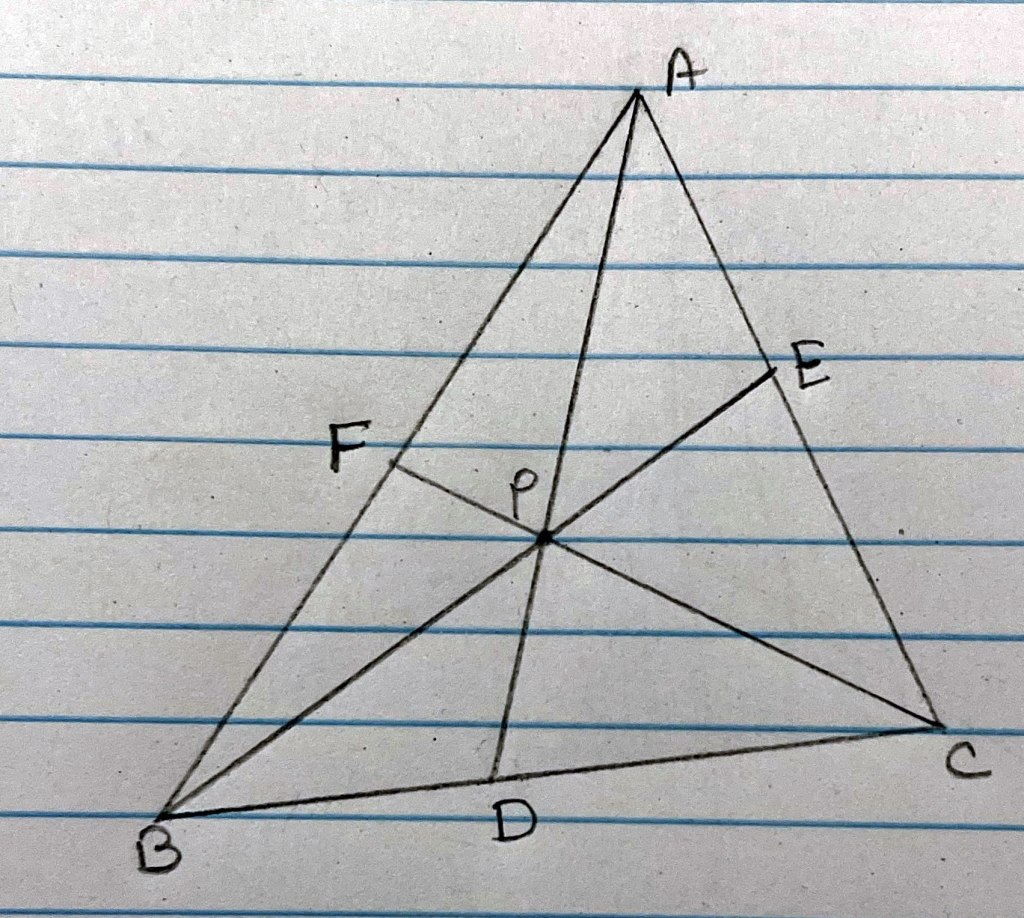
Proof:

= area of figure

Since height from C to base is same for both AFC and BFC (proof in Lemma 1)

Since height from P to base is same for both AFP and BFP

from equation (2) and (3)

similarly if we apply same formulas for E point

Now, adding equation (4) and (5)

In above proof we have used below equation, explanation can be found in Lemma 2 below,

3. Extra Explanation

3.1. explanation equation (2)

Lemma 1 Let there be a point D on line BC of ABC, then

Proof: Let there be AX BC

now,

from above equations:

3.2. explanation equation (6)

Lemma 2 Let there be an interior point P in ABC. Draw AP which meets BC at point D, then

Proof: Let there be AX BC and PY BC,

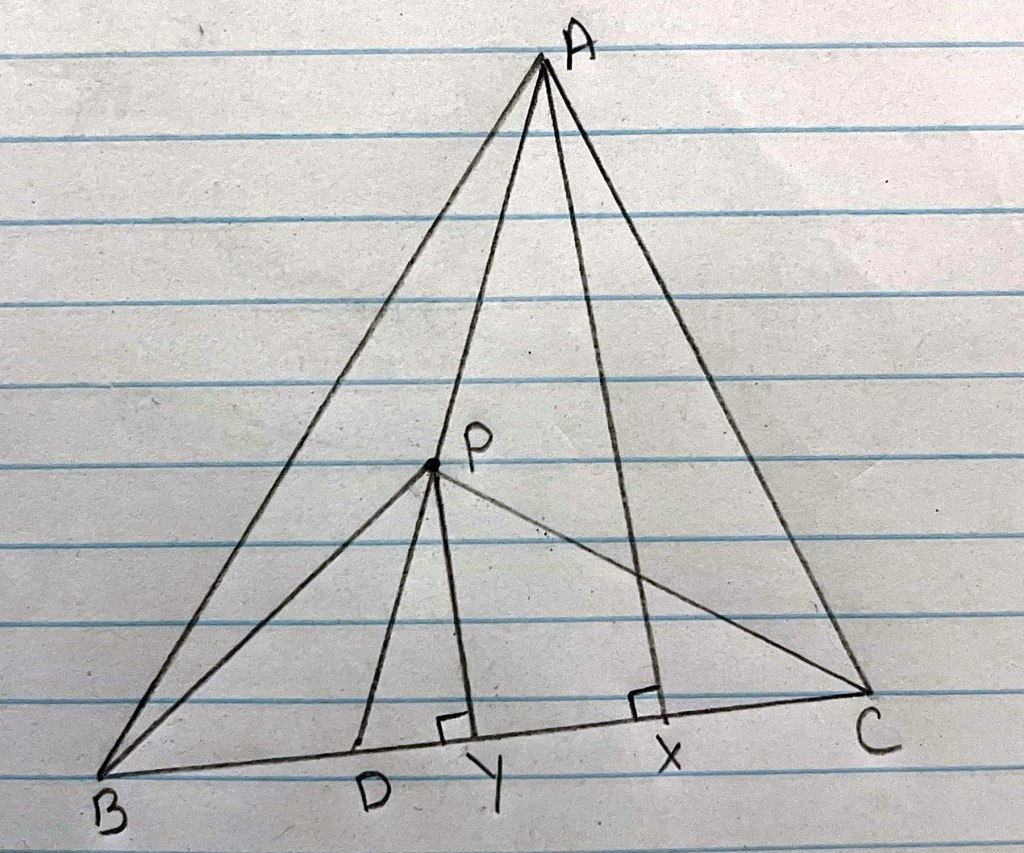
now,

from above equations:

Since,

DAX = DPY [ PY AX],

ADX = PDY and,

AXD = PYD

we can say ADX PDY, so

Hence,

4. Ceva’s Theorem

Theorem: The three lines containing the vertices A, B, and C of ABC and intersecting opposite sides at points D, E, and F, respectively, are concurrent if and only if

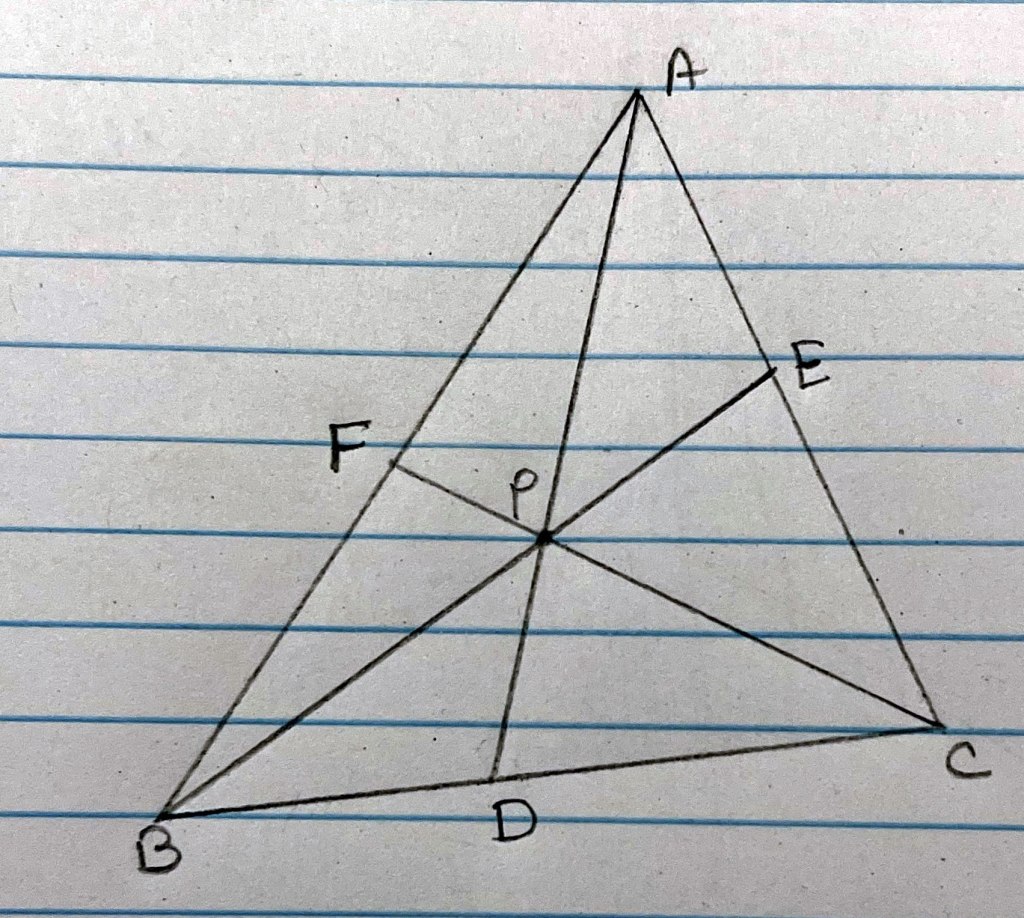
Proof:

Part 1: say line AD, BE and CF are concurrent at point P then prove

Proof: from Lemma 1,

similarly,

Therefore,

(Replace – sign with + sign if A and P are on opposite side of BC)

similarly,

Multiplying 3 equations,

Part 2: Now say we are given, The three lines containing the vertices A, B, and C of ABC and intersecting opposite sides at points D, E, and F such that,

then prove AD, CF and BE are concurrent.

Proof:

We are given,

Now say, AD and BE meet at point P and CP meets AB at F’ which is different from F, Then AD, BE and CF’ are concurrent. And from previous proof

from our hypothesis

But only one point can cut a line segment in given ratio so F = F’, so CF, CE and AD are concurrent