Indian National Mathematics Olympiad 2000 Q1

July 22, 2023

·

Geometry, Maths, MathsOlympiad, Olympiad

1. Problem

The in-circle of triangle ABC touches the sides BC, CA and AB in K, L and M respectively. The line through A and parallel to LK meets MK in P and the line through A and parallel to MK meets LK in Q. Show that the line P Q bisects the sides AB and AC of triangle ABC.

2. Solution

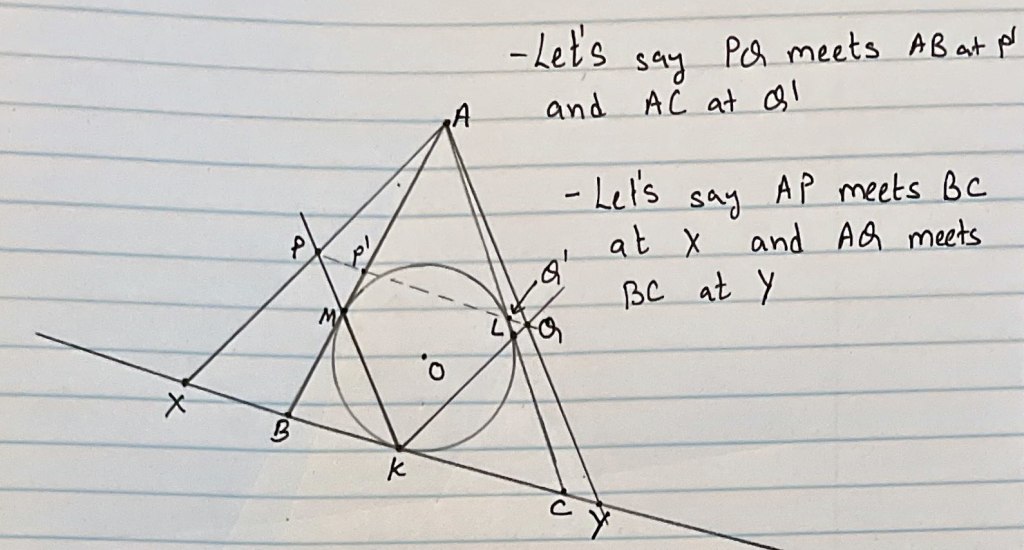
Proof:

Since in-circle touches AB at M and BC at K. So BK and BM are tangents to a circle from B, so

$\displaystyle BK = BM \ \ \ \ \ (1)$

Similarly,

$\displaystyle AL = AM \ \ \ \ \ (2)$

So, ${\Delta}$ BKM is an isosceles triangle,

$\displaystyle \implies \angle BKM = \angle BMK$

Since, MK ${\parallel}$ AY;

$\displaystyle \angle BAY = \angle BMK$

$\displaystyle \angle AYB = \angle MKB$

So,

$\displaystyle \angle AYB = \angle BAY$

So, ${\Delta}$ BAY is an isosceles triangle,

$\displaystyle \implies BY = AB \ \ \ \ \ (3)$

from equation (1) and (3)

$\displaystyle BY-BK = AB - BM$

$\displaystyle KY = AM$

Similarly,

$\displaystyle XK = AL$

but from 2 and above equations;

$\displaystyle KY = KX$

Since, ${KP \parallel AY}$ and ${KY=KX}$

$\displaystyle AP=XP \ \ \ \ \ (4)$

Similarly ${AQ=QY}$ ,

$\displaystyle \implies PQ\parallel XY$

$\displaystyle \implies PQ\parallel BC$

Since ${AP=PX}$ and ${PP' \parallel XB}$ ,

$\displaystyle \implies AP'=P'B$

Similarly, ${AQ'=Q'C}$

Hence PQ bisects both AB and BC
$\Box$

Leave a comment Cancel reply

Instagram

Follow Instagram account as well