Problem
Let ABC be triangle in which AB = AC. Suppose the orthocentre of the triangle lies on the incircle. Find the ratio AB/BC
Solution
Method 1
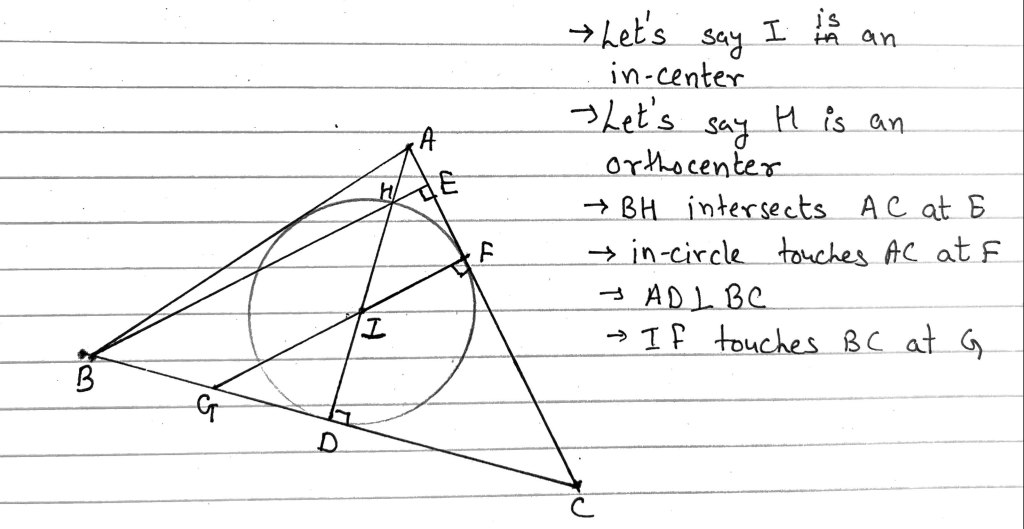
Proof:
Given AB=AC, AD is perpendicular bisector of BC and angle bisector of
So, incenter and orthocenter lies on AD
Since H (Orthocenter) lies on incircle
But and
,
Since,
Since D bisects BC, so
Let’s say BG = x,
So, GD =x; BD = 2x; DC = 2x; BC = 4x; GC = 3x
CF and CD are tangent to incircle, so
Now,
So,
Method 2
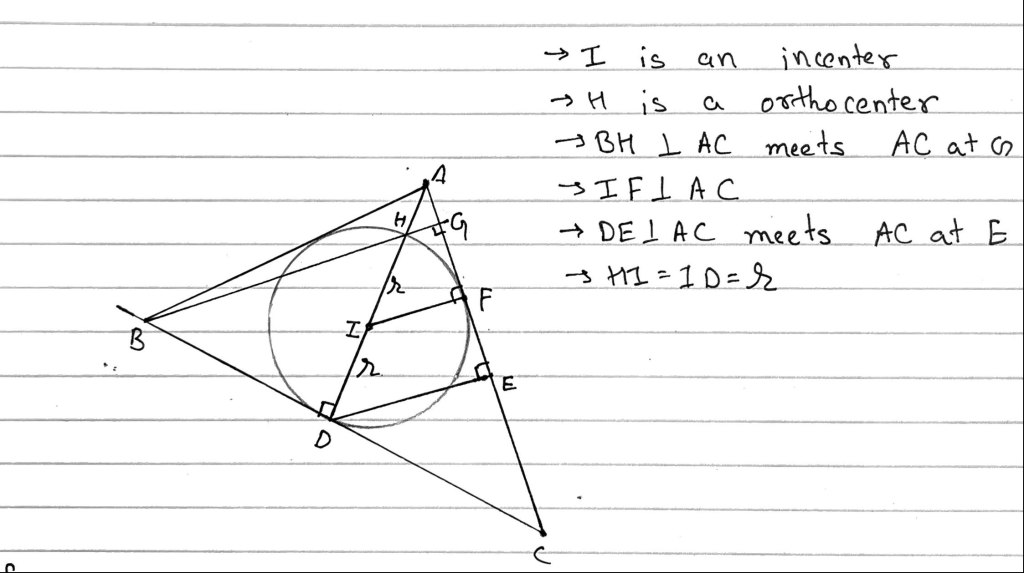
Proof:
Given AB=AC, AD is perpendicular bisector of BC and angle bisector of
So, incenter and orthocenter lies on AD
Since H (Orthocenter) lies on incircle
But and
and
,
Since
Let’s say GF = a,
So, FE =a; GE = 2a; EC = 2a; GC = 4a; FC = 3a
CF and CD are tangent to incircle, so
Now,
So,

Leave a comment